|
Grangerův test kauzality (podmíněnosti) je test používaný pro rozhodnutí o vzájemném ovlivnění časových řad pojmenovaný po britském ekonomu Clivu Williamovi Johnu Grangerovi.
Prinicip
Principem je testování statistické významnosti změny (snížení) nevysvětlené variability autoregresního modelu jedné časové řady, po zahrnutí druhé časové řady to tohoto modelu. Uvažujme autoregresní model (řádu p) časové řady Y:
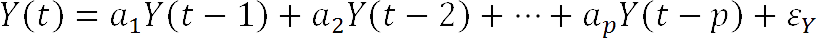
kde Y je predikovaná časová řada, a jsou koeficienty autoregresního modelu a ε je bílý šum.
Nyní tento uvažovaný model rozšiřme přidáním p prvků druhé časové řady X jejíž vzájemnou kauzalitu s řadou Y testujeme:
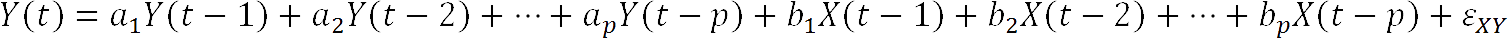
kde X je druhá časová řada.
Zřejmě dojde ke snížení nevysvětlené variability druhého modelu oproti prvnímu. Lze tedy stanovit pro oba modely nevysvětlenou variabilitu jako součet čtverců odchylek mezi predikovanými a skutečnými hodnotami řady a testovat významnost tohoto podílu pomocí F-testu. Statistick významný výsldek pak znamená, že přidání řady X do modelu je podstatné pro zlepšení předpovědi řady Y a řady X tedy podmiňuje řadu Y.
Vzájemným otestováním podmíněnosti mezi řadami X a Y lze dojít ke čtyřem druhům výsledků:
- Řada X nepodmiňuje řadu Y a řada Y nepodmiňuje řadu X - řady jsou nezávislé a nelze hovořit o kauzalitě.
- Řada X podmiňuje řadu Y ale řada Y nepodmiňuje řadu X. Jde o kauzální vztah, kdy řada Y závisí na řadě X (je podmíněná) - což může být dobrý způsob identifikace reálných vazeb např. v ekonomii, když zjišťujeme závislost jednotlivých ukazatelů.
- Opačná varianta 2., kdy řada X závisí na řadě Y.
- Obě řady se podmiňují navzájem - nelze rozhodnout, která závisí na které (která je příčinou a která důsledkem).
Ukázka výpočtu v R
Následující ukázka implementace Grangerova testu ve statistickém softwaru R pracuje s nadfinovanými časovými řadami délky 16, které vstupují do Grangerova testu s p = 1, tj. využívá autoregresní modely 1. řádu (v praxi jsou řáy modelů obvykle podstatně vyšší). Výpočet lze provést buď ručně s nutností definovat oba modely, nebo za použití funkce grangertest, která je součástí balíku lmtests.
# Nadefinovani casovych rad:
rada1<-c( 5, 5, 1,-5,-6,-2, 4, 5, 2,-3,-6,-3, 3, 6, 4,-2)
rada2<-c( 3, 2, 1,-2,-2, 0, 1, 3, 2, 0,-1,-2, 0, 2, 3, 0)
# Autoregresni model radu 1 a jeho rozsirena varianta:
model1 <-lm(rada1[c(-1)]~rada1[c(-16)])
model12<-lm(rada1[c(-1)]~rada1[c(-16)]+rada2[c(-16)])
# F-test:
anova(model1,model12)
# Totez pri pouziti baliku lmtest:
library(lmtest)
grangertest(rada2,rada1,1)
|