|
Theil-Senova regrese (také Sen-Tehilova regrese, Theil-Senův odhad trendu aj.) je neparametrická metoda lineární regrese bodů ve dvou- nebo vícedimenzionálním prostoru. Ve srovnání s běžnou lineární regresí metodou nejmenších čtverců jde o robustní a rychle spočitatelnou metodu lineárního proložení bodů, která není citlivá na odchylky od normálního rozdělení včetně odlehlých hodnot (outlierů).
Princip Theil-Senovy regrese
Princip výpočtu spočívá v nalezení mediánové směrnice všech možných směrnic určených dvojicemi bodů ze zadané množiny a následném dopočtení absolutního členu (interceptu) jako mediánu rozdílů mezi hodnotou bodů v postoru (tj. hodnotou závislé proměnné) a honotou určenou získanou přímkou s nulovým absolutním členem.
Postup výpočtu
V prvním kroku se pro všechny dvojice bodů s (alespoň jednou) vzájemně rozdílnou hodnotou nezávislé proměnné spočítají směrnice přímek, procházejících oběma boy z dvojice. Ze získané množiny reálných čísel je násldně vypočten medián, který představuje směrnici hledané lineární závislosti (přímky). Pro úplný přdpis zbývá zjistit absolutní člen, který je určen jako medián rozdílů mezi hodnotami závislé proměnné v zadaných bodech a hodnotami určenými přímkou s vypočítanou směrnicí a nulovým absolutním členem v týchž bodech.
Ve dvourozměrném případě s nezávislou proměnnou x a závislou proměnnou y jsou nejprve pro množinu n bodů určeny všechny směrnice si,j=(yi-yj)/(xi-xj) a z těchto směrnic je vybrána mediánová směrnice sm:
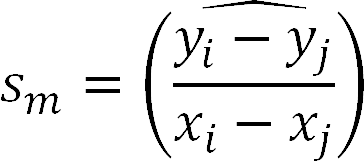
Absolutní člen im se posléze určí jako mediánová hodnota množiny rozdílů mezi skutčnými hodnotami závislé proměnné a hodnotami vypočtené směrnice s nulovým absolutním členem odpovídajícími zadaným hodnotám nezávislé proměnné smxi:
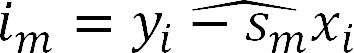
Implementace v R
Následujícíkód uvádí prostou implementaci funkce senthail v jazyce R:
senthail<-function(x,y) {
sl<-rep(NA,(length(x)^2-length(x))/2)
ic<-rep(NA,(length(x)^2-length(x))/2)
for (i in 1:(length(x)-1)) {
for (j in (i+1):length(x)) {
sl[j+length(x)*(i-1)-((i^2+i)/2)]<-(y[j]-y[i])/(x[j]-x[i])
ic[j+length(x)*(i-1)-((i^2+i)/2)]<-(x[j]*y[i]-x[i]*y[j])/(x[j]-x[i])
}
}
slope<-median(sl,na.rm=TRUE)
intercept<-median(ic,na.rm=TRUE)
return(list(slope=slope,intercept=intercept))
}
senthail(c(1,2,3,4,5,6,7,8),c(5,4,5,4,2,3,2,2,1))$slope
senthail(c(1,2,3,4,5,6,7,8),c(5,4,5,4,2,3,2,2,1))$intercept
|